Tổng hợp kiến thức môn Toán 12 (Giải tích)

 MỤC LỤC
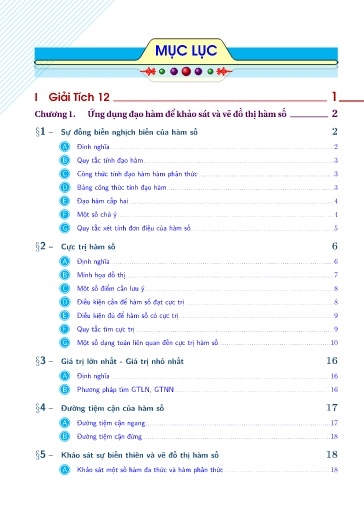
I Giải Tích 12 1
Chương 1. Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số 2
 x1 – Sự đồng biến nghịch biến của hàm số 2
 A Định nghĩa .................................................................................................................. 2
 B Quy tắc tính đạo hàm ................................................................................................. 3
 C Công thức tính đạo hàm hàm phân thức ..................................................................... 3
 D Bảng công thức tính đạo hàm ..................................................................................... 3
 E Đạo hàm cấp hai ........................................................................................................ 4
 F Một số chú ý .............................................................................................................. 4
 G Quy tắc xét tính đơn điệu của hàm số.........................................................................5
 x2 – Cực trị hàm số 6
 A Định nghĩa .................................................................................................................. 6
 B Minh họa đồ thị .......................................................................................................... 7
 C Một số điểm cần lưu ý ................................................................................................ 8
 D Điều kiện cần để hàm số đạt cực trị ............................................................................ 8
 E Điều kiện đủ để hàm số có cực trị ............................................................................... 9
 F Quy tắc tìm cực trị ..................................................................................................... 9
 G Một số dạng toán liên quan đến cực trị hàm số ......................................................... 10
 x3 – Giá trị lớn nhất - Giá trị nhỏ nhất 16
 A Định nghĩa ................................................................................................................ 16
 B Phương pháp tìm GTLN, GTNN ............................................................................... 16
 x4 – Đường tiệm cận của hàm số 17
 A Đường tiệm cận ngang .............................................................................................. 17
 B Đường tiệm cận đứng ................................................................................................ 18
 x5 – Khảo sát sự biến thiên và vẽ đồ thị hàm số 18
 A Khảo sát một số hàm đa thức và hàm phân thức ...................................................... 18 ii | Page MỤC LỤC
 B Đồ thị hàm chứa dấu trị tuyệt đối ............................................................................. 21
 C Một số phép biến đổi đồ thị ...................................................................................... 23
 x6 – Tiếp tuyến 25
 A Tiếp tuyến ................................................................................................................ 25
 | Dạng 6.1: Tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M(x0; y0) ................. 25
 | Dạng 6.2: Tiếp tuyến của đồ thị hàm số y = f(x) có phương cho trước .............. 26
 | Dạng 6.3: Tiếp tuyến của đồ thị hàm số y = f(x) đi qua điểm M(x0; y0) ............ 27
 B Điều kiện tiếp xúc ..................................................................................................... 28
 x7 – Tương giao đồ thị 28
 ax + b
 | Dạng 7.4: Tìm tham số để đồ thị (C): y = cắt đường thẳng (d) tại hai điểm
 cx + d
 28
 | Dạng 7.5: Tìm tham số để đồ thị (C): y = ax3 + bx2 + cx + d cắt đường thẳng (d)
 tại 3 điểm ................................................................................................................. 29
 | Dạng 7.6: Tìm tham số để đồ thị (C): y = ax4 + bx2 + c cắt đường thẳng d tại 4
 điểm ......................................................................................................................... 29
 | Dạng 7.7: Tìm tham số để đồ thị (C): y = f(x) cắt đường thẳng d tại n điểm thỏa
 mãn tính chất nào đó ................................................................................................ 30
 x8 – Điểm đặc biệt của họ đường cong 30
 A Bài toán tìm điểm cố định của họ đường cong .......................................................... 30
 B Bài toán tìm điểm có tọa độ nguyên ......................................................................... 31
 C Bài toán tìm điểm có tính chất đối xứng ................................................................... 31
 D Bài toán tìm điểm đặc biệt, khoảng cách .................................................................. 33
Chương 2. Mũ và Logarit 36
 x1 – Lũy thừa và hàm số lũy thừa 36
 A Khái niệm lũy thừa....................................................................................................36
 n
 B Phương trình x = b ................................................................................................. 37
 C Một số tính chất của căn bậc n ................................................................................ 37
 D Hàm số lũy thừa ....................................................................................................... 37
 x
 E Khảo sát hàm số mũ y = a ..................................................................................... 39
 x2 – Lôgarit 41
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 ii iii | Page MỤC LỤC
 A Khái niệm lôgarit ...................................................................................................... 41
 B Bảng tóm tắt công thức mũ - lôgarit thường gặp ...................................................... 41
 x3 – Bất phương trình mũ và logarit 42
 A Bất phương trình mũ cơ bản ..................................................................................... 42
 B Bất phương trình logarit cơ bản ................................................................................ 43
 x4 – Bài toán lãi suất ngân hàng 44
 A Lãi đơn ..................................................................................................................... 44
 B Lãi kép ...................................................................................................................... 44
 C Tiền gửi hàng tháng .................................................................................................. 45
 D Gửi ngân hàng và rút tiền gửi hàng tháng ................................................................. 45
 E Vay vốn trả góp ........................................................................................................ 45
 F Bài toán tăng lương .................................................................................................. 46
 G Bài toán tăng trưởng dân số ..................................................................................... 46
 H Lãi kép liên tục ......................................................................................................... 46
Chương 3. Nguyên hàm - Tích phân Ứng dụng tích phân 48
 x1 – Nguyên hàm 48
 A Định nghĩa ................................................................................................................ 48
 B Tính chất nguyên hàm .............................................................................................. 48
 C Sự tồn tại nguyên hàm .............................................................................................. 49
 D Bảng nguyên hàm các hàm số thường gặp ................................................................ 49
 E Bảng nguyên hàm mở rộng ....................................................................................... 49
 x2 – Các phương pháp tính nguyên hàm 50
 A Phương pháp đổi biến ............................................................................................... 50
 B Phương pháp nguyên hàm từng phần ........................................................................ 52
 | Dạng 2.8: ........................................................................................................... 53
 | Dạng 2.9: ........................................................................................................... 53
 | Dạng 2.10: ......................................................................................................... 53
 x3 – Tích phân 54
 A Công thức tính tích phân .......................................................................................... 54
 B Tính chất của tích phân ............................................................................................ 54
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 iii iv | Page MỤC LỤC
 x4 – Phương pháp tính tích phân 55
 A Phương pháp đổi biến ............................................................................................... 55
 B Phương pháp tích phân từng phần ............................................................................ 56
 x5 – Tích phân các hàm số sơ cấp cơ bản 57
 A Tích phân hàm hữu tỉ ............................................................................................... 57
 B Tích phân hàm vô tỉ ................................................................................................. 59
 C Tích phân hàm lượng giác ......................................................................................... 62
 x6 – Ứng dụng của tích phân 66
 A Diện tích hình phẳng ................................................................................................. 66
 B Thể tích vật thể và thể tích khối tròn xoay ............................................................... 67
Chương 4. Số phức 70
 x1 – Số phức 70
 A Khái niệm số phức .................................................................................................... 70
 B Hai số phức bằng nhau..............................................................................................70
 C Biểu diễn hình học số phức ....................................................................................... 70
 D Số phức liên hợp ....................................................................................................... 71
 E Mô-đun của số phức ................................................................................................. 71
 x2 – Phép cộng trừ, nhân chia số phức 72
 A Phép cộng và phép trừ số phức ................................................................................. 72
 B Phép nhân số phức....................................................................................................72
 C Chia hai số phức ....................................................................................................... 73
 x3 – Phương trình bậc hai với hệ số thực 73
 A Căn bậc hai của số thực âm ...................................................................................... 73
 B Phương trình bậc hai với hệ số thực .......................................................................... 73
II Hình Học 12 74
Chương 1. Khối đa diện 75
 x1 – Khối lăng trụ và khối chóp 75
 x2 – Khái niệm về hình đa diện và khối đa diện 75
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 iv v | Page MỤC LỤC
 A Khái niệm về hình đa diện ......................................................................................... 75
 B Khái niệm về khối đa diện ......................................................................................... 76
 x3 – Hai đa diện bằng nhau 77
 A Phép dời hình trong không gian ................................................................................ 77
 B Hai hình bằng nhau ................................................................................................... 78
 x4 – Phân chia và lắp ghép các khối đa diện 78
 x5 – Khối đa diện lồi 79
 A Khối đa diện lồi.........................................................................................................79
 B Khối đa diện đều ....................................................................................................... 80
 C Một số kết quả quan trọng về khối đa diện lồi...........................................................81
 x6 – Thể tích khối đa diện 82
 A Thể tích khối chóp .................................................................................................... 82
 B Thể tích khối lăng trụ ............................................................................................... 82
 C Thể tích khối hộp chữ nhật ....................................................................................... 83
 D Thể tích khối lập phương .......................................................................................... 83
 E Tỉ số thể tích ............................................................................................................ 83
 F Một số chú ý về độ dài các đường đặc biệt ............................................................... 84
 x7 – Các công thức hình phẳng 84
 A Hệ thức lượng trong tam giác ................................................................................... 84
 x8 – Một số công thức tính nhanh thể tích khối chóp thường gặp 86
 x9 – Các công thức đặc biệt của thể tích tứ diện 89
Chương 2. Mặt nón - mặt trụ - mặt cầu 92
 x1 – Mặt nón tròn xoay và khối nón 92
 A Mặt nón tròn xoay .................................................................................................... 92
 B Khối nón ................................................................................................................... 92
 C Thiết diện khi cắt bởi mặt phẳng .............................................................................. 93
 x2 – Mặt trụ tròn xoay và khối trụ 94
 A Mặt trụ ..................................................................................................................... 94
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 v vi | Page MỤC LỤC
 B Hình trụ tròn xoay và khối trụ tròn xoay ................................................................... 95
 x3 – Mặt cầu và khối cầu 96
 A Mặt cầu .................................................................................................................... 96
 B Vị trí tương đối của mặt cầu và mặt phẳng ............................................................... 96
 C Vị trí tương đối của mặt cầu và đường thẳng ............................................................ 97
 D Đường kinh tuyến và vĩ tuyến của mặt cầu ................................................................ 98
 x4 – Một số dạng toán và công thức giải nón và trụ 99
 A Bài toán mặt nón ...................................................................................................... 99
 B Một số dạng toán và công thức giải bài toán mặt trụ .............................................. 105
 x5 – Một số dạng toán và công thức giải bài toán mặt cầu 108
 A Mặt cầu ngoại tiếp khối đa diện .............................................................................. 108
 B Kỹ thuật xác định mặt cầu ngoại tiếp hình chóp......................................................112
 C Kỹ năng xác định trục đường tròn ngoại tiếp đa giác đáy ........................................ 113
 D Kỹ thuật sử dụng hai trục xác định tâm mặt cầu ngoại tiếp đa diện ........................ 115
 E Tổng kết các dạng tìm tâm và bán kính mặt cầu ..................................................... 115
 F Dạng 6 .................................................................................................................... 118
 x6 – Tổng hợp các công thức đặc biệt về khối tròn xoay 118
 A Chỏm cầu ............................................................................................................... 118
 B Hình trụ cụt ............................................................................................................ 118
 C Hình nêm loại 1.......................................................................................................119
 D Hình nêm loại 2.......................................................................................................119
 E Parabol bậc hai - Paraboloid....................................................................................120
 F Diện tích Elip và thể tích khối tròn xoay sinh bởi Elip ............................................. 120
 G Diện tích hình vành khăn ........................................................................................ 121
 H Thể tích hình xuyến (phao) ..................................................................................... 121
Chương 3. Hệ tọa độ trong không gian 122
 x1 – Hệ tọa độ trong không gian 122
 A Các khái niệm và tính chất ...................................................................................... 122
 B Phương pháp giải một số bài toán thường gặp ........................................................ 125
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 vi vii | Page MỤC LỤC
x2 – Mặt phẳng 126
 A Các khái niệm và tính chất ...................................................................................... 126
 B Viết Phương Trình Mặt Phẳng ................................................................................ 127
 C Vị trí tương đối của hai mặt phẳng..........................................................................130
 D Khoảng cách và hình chiếu ...................................................................................... 130
 E Góc giữa hai mặt phẳng .......................................................................................... 130
 F Vị trí tương đối giữa mặt phẳng và mặt cầu. Phương trình mặt phẳng tiếp xúc mặt cầu.
 131
x3 – Đường thẳng 131
 A Phương trình của đường thẳng ................................................................................ 131
 B Vị trí tương đối ....................................................................................................... 132
 C Góc trong không gian .............................................................................................. 135
 D Khoảng cách ........................................................................................................... 136
 E Lập phương trình đường thẳng ................................................................................ 138
 F Vị trí tương đối ....................................................................................................... 141
 G Khoảng cách ........................................................................................................... 142
 H Góc ......................................................................................................................... 143
x4 – Mặt cầu 143
 A Phương trình mặt cầu ............................................................................................. 143
 B Giao của mặt cầu và mặt phẳng .............................................................................. 144
 C Một số bài toán liên quan ....................................................................................... 144
x5 – Một số bài toán giải nhanh cực trị không gian 147
 A Dạng 1. ................................................................................................................... 147
 B Dạng 2. ................................................................................................................. 148
 C Dạng 3. ................................................................................................................. 148
 D Dạng 4. ................................................................................................................... 148
 E Dạng 5. ................................................................................................................. 148
 F Dạng 6. ................................................................................................................... 149
 G Dạng 7. ................................................................................................................. 149
 H Dạng 8. ................................................................................................................... 149
 I Dạng 9. ................................................................................................................. 150
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 vii viii | Page MỤC LỤC
 J Dạng 10. ................................................................................................................. 150
Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 viii PHẦN
GIẢI TÍCH 12 I
 34 21
 6 49
 26 17 4
 3 35 50
 13 19
 32 25 16
 23 7
 37 39 42
 45 48
 8 27
 46 18 41 2
 33
 28 15
12
 9 30 5
 43 29 38
 24 47
 40 44
 10
 1 14 20 22
 113631 CHƯƠNG
 ỨNG DỤNG ĐẠO
 1 HÀM ĐỂ KHẢO SÁT VÀ
 VẼ ĐỒ THỊ HÀM SỐ
 hủ đề
 C
 1 SỰ ĐỒNG BIẾN NGHỊCH BIẾN CỦA HÀM SỐ
 A. ĐỊNH NGHĨA
 Ký hiệu K là khoảng hoặc đoạn hoặc nửa khoảng. Giả sử hàm số y = f(x) xác định trên K, ta có
 • Hàm số y = f(x) được gọi là đồng biến (tăng) trên K nếu với mọi x1, x2 ∈ K, x1 < x2 thì
 f (x1) < f (x2).
 • Hàm số y = f(x) được gọi là nghịch biến (giảm) trên K nếu với mọi x1, x2 ∈ K, x1 < x2
 thì f (x1) > f (x2).
 Hàm số đồng biến hoặc nghịch biến trên K được gọi chung là đơn điệu trên K.
 Nhận xét.
 • Hàm số f(x) đồng biến trên K khi và chỉ khi
 y
 f (x2) − f (x1)
 > 0, ∀x1, x2 ∈ K, x1 6= x2.
 x2 − x1 O
 x
 Khi đó đồ thị của hàm số đi lên từ trái sang phải.
 • Hàm số f(x) nghịch biến trên K khi và chỉ khi
 y
 f (x2) − f (x1)
 < 0, ∀x1, x2 ∈ K, x1 6= x2.
 x2 − x1
 O x
 Khi đó đồ thị của hàm số đi xuống từ trái sang phải.
 • Nếu f 0(x) > 0, ∀x ∈ (a; b) thì hàm số f(x) đồng biến trên khoảng (a; b). 3 | Page 1. Sự đồng biến nghịch biến của hàm số
 • Nếu f 0(x) < 0, ∀x ∈ (a; b) thì hàm số f(x) nghịch biến trên khoảng (a; b).
 • Nếu f 0(x) = 0, ∀x ∈ (a; b) thì hàm số f(x) không đổi trên khoảng (a; b).
 • Nếu hàm số f(x) đồng biến trên khoảng (a; b) thì f 0(x) ≥ 0, ∀x ∈ (a; b).
 • Nếu hàm số f(x) nghịch biến trên khoảng (a; b) thì f 0(x) ≤ 0, ∀x ∈ (a; b).
 • Nếu thay đổi khoảng (a; b) bằng một đoạn hoặc nửa khoảng thì phải bổ sung thêm giả
 thiết hàm số f(x) liên tục trên đoạn hoặc nửa khoảng đó.
 B. QUY TẮC TÍNH ĐẠO HÀM
Cho u = u(x), v = v(x) và C là hằng số.
 • Tổng, hiệu: (u ± v)0 = u0 ± v0.
 • Tích: (uv)0 = u0v + v0u ⇒ (C · u)0 = C · u0.
 u0 u0 · v − v0 · u ÅC ã0 C · u0
 • Thương: = , (v 6= 0) ⇒ = − .
 v v2 u u2
 0 0 0
 • Đạo hàm hàm hợp: Nếu y = f(u) với u = u(x) thì yx = yu · ux.
 C. CÔNG THỨC TÍNH ĐẠO HÀM HÀM PHÂN THỨC
 ax + b Åax + bã0 ad − bc
 • y = ⇒ y0 = = .
 cx + d cx + d (cx + d)2
 a b a c b c
   2    
   x + 2   x +  
  0 0  0 0  0 0
 ax2 + bx + c Å ax2 + bx + c ã0 a b  a c  b c 
 • y = ⇒ y0 = = .
 a0x2 + b0x + c0 a0x2 + b0x + c0 (a0x2 + b0x + c0)2
 D. BẢNG CÔNG THỨC TÍNH ĐẠO HÀM
 Hàm sơ cấp Hàm hợp
 (C)0 = 0,(C là hằng số)
 (xα)0 = α · xα−1 (uα)0 = α · uα−1 · u0
 Å 1 ã0 1 Å 1 ã0 u0
 = − , (x 6= 0) = − , (u 6= 0)
 x x2 u u2
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 3 4 | Page 1. Sự đồng biến nghịch biến của hàm số
 √ 1 √ u0
 ( x)0 = √ , (x > 0) ( u)0 = √ , (u > 0)
 2 x 2 u
 (sin x)0 = cos x (sin u)0 = u0 · cos u
 (cos x)0 = − sin x (cos u)0 = −u0 · sin u
 1 u0
 (tan x)0 = (tan u)0 =
 cos2 x cos2 u
 1 u0
 (cot x)0 = − (cot u)0 = −
 sin2 x sin2 u
 (sinn x)0 = n · sinn−1 x · cos x (sinn u)0 = n · u0 · sinn−1 u · cos u
 (cosn x)0 = −n · cosn−1 x · sin x (cosn u)0 = −n · u0 · cosn−1 u · sin u
 1 1
 (tann x)0 = n · tann−1 x · (tann u)0 = n · u0 · tann−1 u ·
 cos2 x cos2 u
 1 1
 (cotn x)0 = −n · cotn−1 x · (cotn u)0 = −n·u0 ·cotn−1 u·
 sin2 x sin2 u
 (ex)0 = ex (eu)0 = u0 · eu
 (ax)0 = ax · ln a (au)0 = u0 · au · ln a
 1 u0
 (ln |x|)0 = , (x 6= 0) (ln |u|)0 = , (u 6= 0)
 x u
 1 u0
 (log |x|)0 = , (x 6= 0) (log |u|)0 = , (u 6= 0)
 a x ln a a u · ln a
 E. ĐẠO HÀM CẤP HAI
 1. Định nghĩa
 f 00(x) = [f 0(x)]0 .
 2. Ý nghĩa cơ học
 00
Gia tốc tức thời của chuyển động s = f(t) tại thời điểm t0 là a (t0) = f (t0).
 3. Đạo hàm cấp cao
 0
 (n) î (n−1) ó
 f (x) = f (x) , (n ∈ N, n ≥ 2).
 F. MỘT SỐ CHÚ Ý
 • Nếu hàm số f(x) và g(x) cùng đồng biến (nghịch biến) trên K thì hàm số f(x) + g(x) cũng
 đồng biến (nghịch biến) trên K. Tính chất này có thể không đúng đối với hiệu f(x) − g(x).
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 4 5 | Page 1. Sự đồng biến nghịch biến của hàm số
 • Nếu hàm số f(x) và g(x) là các hàm số dương và cùng đồng biến (nghịch biến) trên K thì
 hàm số f(x) · g(x) cũng đồng biến (nghịch biến) trên K. Tính chất này có thể không đúng
 khi các hàm số f(x), g(x) không là các hàm số dương trên K.
Nhận xét. Cho hàm số u = u(x) xác định với mọi x ∈ (a; b) và u(x) ∈ (c; d). Hàm số f [u(x)]
cũng xác định với x ∈ (a; b).
 • Giả sử hàm số u = u(x) đồng biến với x ∈ (a; b). Khi đó, hàm số f [u(x)] đồng biến với
 x ∈ (a; b) khi và chỉ khi f(u) đồng biến với u ∈ (c; d).
 • Giả sử hàm số u = u(x) nghịch biến với x ∈ (a; b). Khi đó, hàm số f [u(x)] nghịch biến với
 x ∈ (a; b) khi và chỉ khi f(u) nghịch biến với u ∈ (c; d).
 G. QUY TẮC XÉT TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
 Giả sử hàm số f có đạo hàm trên K.
 • Nếu f 0(x) ≥ 0 với mọi x ∈ K và f 0(x) = 0 chỉ tại một số hữu hạn điểm x ∈ K thì
 hàm số f đồng biến trên K.
 • Nếu f 0(x) ≤ 0 với mọi x ∈ K và f 0(x) = 0 chỉ tại một số hữu hạn điểm x ∈ K thì
 hàm số f nghịch biến trên K.
 Chú ý
 ax + b Å dã
 • Đối với hàm phân thức hữu tỉ y = , x 6= − thì dấu = khi xét dấu đạo
 cx + d c
 hàm y0 không xảy ra.
 • Giả sử y = f(x) = ax3 + bx2 + cx + d ⇒ f 0(x) = 3ax2 + 2bx + c.
 – Hàm số đồng biến trên R khi và chỉ khi
 2 8
 0
 6
 6
 6 :∆ ≤ 0
 6
 6 8
 0 6
 f (x) ≥ 0, ∀x ∈ R ⇔ 6 >a = 0
 6 >
 6 <
 6 b = 0
 6 >
 4 >
 :>c > 0.
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 5 6 | Page 2. Cực trị hàm số
 – Hàm số nghịch biến trên R khi và chỉ khi
 2 8
 <a < 0
 6
 6
 6 :∆ ≤ 0
 6
 6 8
 0 6
 f (x) ≤ 0, ∀x ∈ R ⇔ 6 >a = 0
 6 >
 6 <
 6 b = 0
 6 >
 4 >
 :>c < 0.
 Trường hợp a = b = 0 thì c phải khác 0. Vì nếu a = b = c = 0 thì f(x) = d có đồ
 thị là đường thẳng song song hoặc trùng với Ox nên không đơn điệu.
 • Với dạng toán tìm tham số m để hàm số bậc ba đơn điệu một chiều trên khoảng có
 độ dài bằng ` ta giải như sau
 – Bước 1. Tính y0 = f 0(x; m) = ax2 + bx + c.
 0
 – Bước 2. Hàm số đơn điệu trên (x1; x2) khi và chỉ khi y = 0 có 2 nghiệm phân
 8
 <a 6= 0
 biệt. Điều kiện tương đương là (∗)
 :∆ > 0.
 – Bước 3. Hàm số đơn điệu trên khoảng có độ dài bằng ` khi và chỉ khi
 2 2 2 2
 |x1 − x2| = ` ⇔ (x1 + x2) − 4x1x2 = ` ⇔ S − 4P = ` . (∗∗)
 – Bước 4. Giải (∗) và giao với (∗∗) để suy ra giá trị m cần tìm.
 hủ đề
 C
 2 CỰC TRỊ HÀM SỐ
 A. ĐỊNH NGHĨA
Giả sử hàm f xác định trên tập K và x0 ∈ K. Ta nói
 • x0 là điểm cực tiểu của hàm số f nếu tồn tại một khoảng (a; b) chứa x0 sao cho (a; b) ⊂ K
 và f(x) > f(x0), ∀x ∈ (a; b) \{x0}. Khi đó f(x0) được gọi là giá trị cực tiểu của hàm số
 f.
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 6 7 | Page 2. Cực trị hàm số
 • x0 là điểm cực đại của hàm số f nếu tồn tại một khoảng (a; b) chứa x0 sao cho (a; b) ⊂ K
 và f(x) < f(x0), ∀x ∈ (a; b) \{x0}. Khi đó f(x0) được gọi là giá trị cực đại của hàm số f.
 • Điểm cực đại và cực tiểu gọi chung là điểm cực trị của hàm số và điểm cực trị phải là
 một điểm trong tập hợp K.
 • Giá trị cực đại và giá trị cực tiểu gọi chung là giá trị cực trị (hay cực trị) của hàm số.
 • Nếu x0 là điểm cực trị của hàm số thì điểm (x0; f(x0)) được gọi là điểm cực trị của đồ
 thị hàm số f.
Nhận xét.
 • Giá trị cực đại (cực tiểu) f(x0) nói chung không phải là giá trị lớn nhất (nhỏ nhất) của hàm
 số f trên tập D; f(x0) chỉ là giá trị lớn nhất (nhỏ nhất) của hàm số f trên một khoảng
 (a; b) nào đó chứa x0 hay nói cách khác khi x0 là điểm cực đại (cực tiểu) sẽ tồn tại khoảng
 (a; b) chứa x0 sao cho f(x0) là giá trị lớn nhất (nhỏ nhất) của hàm số f trên khoảng (a; b).
 • Hàm số f có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập K. Hàm số có thể không
 có cực trị trên một tập cho trước.
 B. MINH HỌA ĐỒ THỊ
Với (a; b) là khoảng chứa tất cả các số thực thỏa a < x < b.
 y y
 (c; f(c))
 f(c)
 f(c)
 (c; f(c))
 O c x O c x
 Hàm số f đạt cực đại tại x = c Hàm số f đạt cực tiểu tại x = c
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 7 8 | Page 2. Cực trị hàm số
C. MỘT SỐ ĐIỂM CẦN LƯU Ý
 Điểm cực
 Giá trị cực
 đại của đồ y
 đại (cực đại)
 thị
 của hàm số
 yCĐ
 Điểm cực Điểm cực
 đại của hàm tiểu của
 số hàm số
 xCT
 xCĐ O x
 yCT
 Giá trị cực Điểm cực
 tiểu (cực tiểu) tiểu của đồ
 của hàm số thị
 • Hàm số f có cực trị khi và chỉ khi y0 đổi dấu.
 • Hàm số f không có cực trị khi và chỉ khi y0 không đổi dấu.
 • Hàm số f chỉ có 1 cực trị khi và chỉ khi y0 đổi dấu 1 lần.
 • Hàm số f có 2 cực trị (cực đại và cực tiểu) khi và chỉ khi y0 đổi dấu 2 lần.
 • Hàm số f có 3 cực trị khi và chỉ khi y0 đổi dấu 3 lần.
 • Đối với một hàm số bất kỳ, hàm số chỉ có thể đạt cực trị tại những điểm mà tại đó đạo hàm
 triệt tiêu hoặc đạo hàm không xác định.
 • Cách gọi tên: cực trị, điểm cực trị của hàm số, điểm cực trị của đồ thị hàm số,. . .
D. ĐIỀU KIỆN CẦN ĐỂ HÀM SỐ ĐẠT CỰC TRỊ
 ǥ Định lí 2.1. Giả sử hàm số y = f(x) đạt cực trị tại điểm x0. Khi đó, nếu y = f(x) có
 0
 đạo hàm tại điểm x0 thì f (x0) = 0.
Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 8 9 | Page 2. Cực trị hàm số
 Chú ý
 Chú ý
 0
 • Đạo hàm f (x) có thể bằng 0 tại điểm x0 nhưng hàm số f không đạt cực trị tại điểm x0.
 • Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm.
 • Hàm số chỉ có thể đạt cực trị tại một điểm mà tại đó đạo hàm của hàm số bằng 0 hoặc
 tại đó hàm số không có đạo hàm.
 E. ĐIỀU KIỆN ĐỦ ĐỂ HÀM SỐ CÓ CỰC TRỊ
 ǥ Định lí 2.2. Giả sử hàm số f đạt cực trị tại điểm x0. Khi đó, nếu hàm số f có đạo hàm
 0
 tại điểm x0 thì f (x0) = 0.
 0 0
 • Nếu f (x) > 0 trên khoảng (x0 − h; x0) và f (x) < 0 trên khoảng (x0; x0 + h) thì x0 là
 một điểm cực đại của hàm số f(x).
 0 0
 • Nếu f (x) 0 trên khoảng (x0; x0 + h) thì x0 là
 một điểm cực tiểu của hàm số f(x).
 F. QUY TẮC TÌM CỰC TRỊ
 1. Quy tắc 1
Để tìm cực trị của hàm số y = f(x) ta thực hiện theo các bước sau
 • Bước 1: Tìm tập xác định. Tìm f 0(x).
 • Bước 2: Tìm các điểm xi (i = 1; 2; ...) mà tại đó đạo hàm của hàm số bằng 0 hoặc hàm số
 liên tục nhưng không có đạo hàm.
 0 0
 • Bước 3: Lập bảng biến thiên hoặc bảng xét dấu của f (x). Nếu f (x) đổi dấu khi đi qua xi
 thì hàm số đạt cực trị tại xi.
 ǥ Định lí 2.3. Giả sử hàm số y = f(x) có đạo hàm cấp hai trong khoảng (x0 − h; x0 + h)
 với h > 0. Khi đó
 0 00
 • Nếu f (x0) = 0, f (x0) < 0 thì hàm số f đạt cực đại tại x0.
 0 00
 • Nếu f (x0) = 0, f (x0) > 0 thì hàm số f đạt cực tiểu tại x0.
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 9 10 | Page 2. Cực trị hàm số
Từ định lí trên, ta có một quy tắc khác để tìm cực trị của hàm số.
 2. Quy tắc 2
Để tìm cực trị của hàm số y = f(x) ta thực hiện theo các bước sau
 • Bước 1: Tìm tập xác định. Tìm f 0(x).
 0
 • Bước 2: Tìm các nghiệm xi (i = 1; 2; ...) của phương trình f (x) = 0.
 00 00
 • Bước 3: Tính f (x) và tính f (xi).
 00
 – Nếu f (xi) < 0 thì hàm số f đạt cực đại tại điểm xi.
 00
 – Nếu f (xi) > 0 thì hàm số f đạt cực tiểu tại điểm xi.
 G. MỘT SỐ DẠNG TOÁN LIÊN QUAN ĐẾN CỰC TRỊ HÀM SỐ
 1. Cực trị của hàm số bậc ba y = ax3 + bx2 + cx + d, (a 6= 0)
 a) Tìm điều kiện để hàm số có cực đại, cực tiểu thỏa mãn hoành độ cho trước.
 (a) Bài toán tổng quát
 Cho hàm số y = f(x; m) = ax3 + bx2 + cx + d. Tìm tham số m để hàm số có cực đại,
 cực tiểu tại x1, x2 thỏa mãn điều kiện K cho trước.
 Phương pháp
 • Bước 1: Tập xác định D = R.
 Đạo hàm y0 = 3ax2 + 2bx + c = Ax2 + Bx + C.
 • Bước 2: Hàm số có cực trị (hay có hai cực trị, hai cực trị phân biệt hay có cực
 đại và cực tiểu) khi và chỉ khi y0 = 0 có hai nghiệm phân biệt và y0 đổi dấu qua
 hai nghiệm đó.
 Phương trình y0 = 0 có hai nghiệm phân biệt khi và chỉ khi
 8 8
 <A = 3a 6= 0 <a 6= 0
 ⇔ ⇒ m ∈ D1.
 2 2 2
 :∆y0 = B − 4AC = 4b − 12ac > 0 :b − 3ac > 0
 0
 • Bước 3: Gọi x1, x2 là hai nghiệm của phương trình y = 0. Khi đó
 8 B 2b
 >S = x + x = − = −
 < 1 2 A 3a
 C c
 :>P = x x = = .
 1 2 A 3a
 Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 10 11 | Page 2. Cực trị hàm số
 • Bước 4: Biến đổi điều kiện K về dạng tổng S và tích P . Từ đó giải ra tìm được
 m ∈ D2.
 • Bước 5: Kết luận các giá trị m thỏa mãn m ∈ D1 ∩ D2.
 Chú ý
 Hàm số bậc ba y = ax3 + bx2 + cx + d (a 6= 0). Ta có y0 = 3ax2 + 2bx + c.
 • Hàm số không có cực trị khi b2 − 3ac ≤ 0.
 • Hàm số có hai điểm cực trị khi b2 − 3ac > 0.
 (b) Điều kiện để hàm số có các điểm cực trị cùng dấu, trái dấu.
 • Hàm số có hai điểm cực trị trái dấu khi và chỉ khi phương trình y0 = 0 có hai
 nghiệm phân biệt trái dấu, tức là
 A · C = 3ac < 0 ⇔ ac < 0.
 • Hàm số có hai điểm cực trị cùng dấu khi và chỉ khi phương trình y0 = 0 có hai
 nghiệm phân biệt cùng dấu, tức là
 8
 0
 C
 >P = x x = > 0.
 : 1 2 A
 • Hàm số có hai điểm cực trị cùng dấu dương khi và chỉ khi phương trình y0 = 0 có
 hai nghiệm dương phân biệt, tức là
 8
 >∆y0 > 0
 >
 <> B
 S = x1 + x2 = − > 0
 > A
 > C
 >P = x x = > 0.
 : 1 2 A
 • Hàm số có hai điểm cực trị cùng dấu âm khi và chỉ khi phương trình y0 = 0 có hai
 nghiệm âm phân biệt, tức là
 8
 >∆y0 > 0
 >
 <> B
 S = x1 + x2 = − < 0
 > A
 > C
 >P = x x = > 0.
 : 1 2 A
Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 11 12 | Page 2. Cực trị hàm số
 ³
 x1 < α < x2
 (c) Tìm điều kiện để hàm số có hai điểm cực trị x1, x2 thỏa mãn x1 < x2 < α
 α < x1 < x2.
 • Hai điểm cực trị x1, x2 thỏa mãn x1 < α < x2 khi và chỉ khi
 2
 (x1 − α)(x2 − α) < 0 ⇔ x1x2 − α(x1 + x2) + α < 0.
 • Hai điểm cực trị x1, x2 thỏa mãn x1 < x2 < α khi và chỉ khi
 8 8 2
 0 0
 ⇔
 :x1 + x2 < 2α :x1 + x2 < 2α.
 • Hai điểm cực trị x1, x2 thỏa mãn α < x1 < x2 khi và chỉ khi
 8 8 2
 0 0
 ⇔
 :x1 + x2 > 2α :x1 + x2 > 2α.
 b) Tìm điều kiện để đồ thị hàm số có các điểm cực đại, cực tiểu nằm cùng phía, khác phía so
 với một đường thẳng.
 (a) Vị trí tương đối của hai điểm với đường thẳng.
 Cho hai điểm A(xA; yA), B(xB; yB) và đường thẳng ∆: ax + by + c = 0.
 • Nếu (axA + byA + c)(axB + byB + C) < 0 thì hai điểm A, B nằm về hai phía so với
 đường thẳng ∆.
 • Nếu (axA + byA + c)(axB + byB + C) > 0 thì hai điểm A, B nằm cùng phía so với
 đường thẳng ∆.
 (b) Một số trường hợp đặc biệt.
 • Các điểm cực trị của đồ thị nằm cùng về một phía đối với trục Oy khi và chỉ khi
 hàm số có 2 điểm cực trị cùng dấu, tức là phương trình y0 = 0 có hai nghiệm phân
 biệt cùng dấu.
 • Các điểm cực trị của đồ thị nằm cùng về hai phía đối với trục Oy khi và chỉ khi
 hàm số có 2 điểm cực trị trái dấu, tức là phương trình y0 = 0 có hai nghiệm trái
 dấu.
 • Các điểm cực trị của đồ thị nằm cùng về một phía đối với trục Ox khi và chỉ khi
 0
 phương trình y = 0 có hai nghiệm phân biệt và yCĐ · yCT > 0.
Ô Thạc Sĩ: Lương Văn Huy - ĐT: 0909127555
 12